Redis实践之签到统计

Redis实践之签到统计

1.BitMap介绍

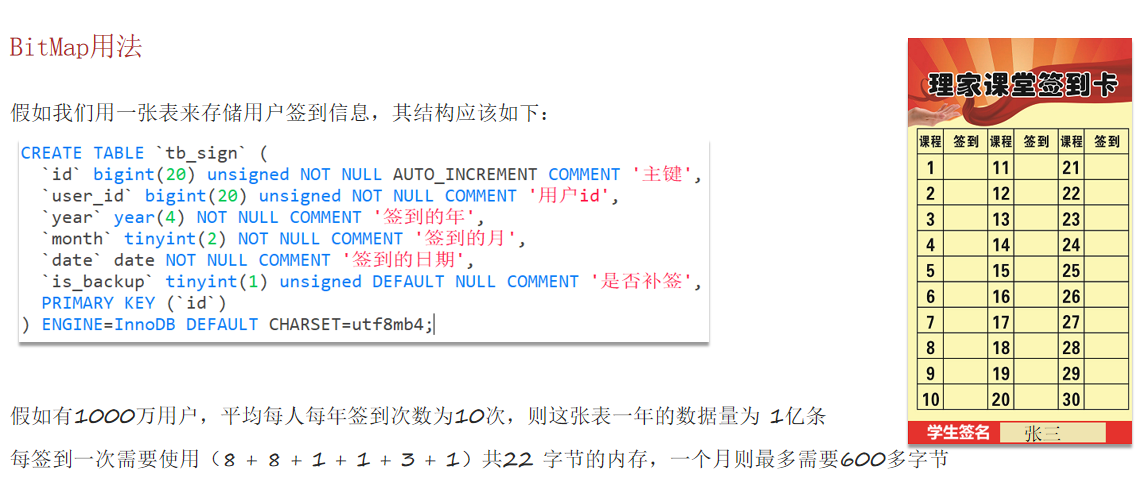
image-20240113104621780

image-20240113105102867

image-20240113105137296

2.签到功能

image-20240113105207927 

1
2
3
4
5
6
7
8
9
10
11
12
13
public Result sign() {
    // 获取当前用户ID
    Long userId = UserHolder.getUser().getId();
    // 获取日期信息
    LocalDateTime now = LocalDateTime.now();
    // 组装位图键
    String key = "sign:" + userId + now.format(DateTimeFormatter.ofPattern(":yyyyMM"));
    // 获取本月的第几天
    int dayOfMonth = now.getDayOfMonth();
    // 利用位图进行用户的本月签到
    stringRedisTemplate.opsForValue().setBit(key, dayOfMonth - 1, true);
    return Result.ok();
}

3.签到统计

image-20240113105332762

image-20240113105416457 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public Result signCount() {
    // 获取当前用户ID
    Long userId = UserHolder.getUser().getId();
    // 获取日期信息
    LocalDateTime now = LocalDateTime.now();
    // 组装位图键
    String key = "sign:" + userId + now.format(DateTimeFormatter.ofPattern(":yyyyMM"));
    // 获取本月的第几天
    int dayOfMonth = now.getDayOfMonth();
    // 获取用户本月的签到记录
    List<Long> result = stringRedisTemplate.opsForValue().bitField(key, BitFieldSubCommands.create().get(BitFieldSubCommands.BitFieldType.unsigned(dayOfMonth)).valueAt(0));
    if (result == null || result.isEmpty()) {
        return Result.ok(0);
    }
    Long num = result.get(0);
    // 统计连续签到天数
    int count = 0;
    while ((num & 1) != 0) {
        count++;
        num >>>= 1;
    }
    return Result.ok(count);
}

4.UV统计

Redis中的HLL是基于string结构实现的，单个HLL的内存永远小于16kb，内存占用低的令人发指！作为代价，其测量结果是概率性的，有小于0.81％的误差。不过对于UV统计来说，这完全可以忽略。

image-20240113113728235

5.HyperLogLog原理

参考文章：探索HyperLogLog算法（含Java实现） - 简书 (jianshu.com)

5.1概率原理

基数就是指一个集合中不同值的数目，比如[a,b,c,d]的基数就是4，[a,b,c,d,a]的基数还是4，因为a重复了一个不算。基数也可以称之为Distinct Value，简称DV。下文中可能有时候称呼为基数，有时候称之为DV，但都是同一个意思。HyperLogLog算法就是用来计算基数的。

HyperLogLog本质上来源于生活中一个小的发现，假设你抛了很多次硬币，你告诉在这次抛硬币的过程中最多只有两次扔出连续的反面，让我猜你总共抛了多少次硬币，我敢打赌你抛硬币的总次数不会太多，相反，如果你和我说最多出现了100次连续的反面，那么我敢肯定扔硬盘的总次数非常的多，甚至我还可以给出一个估计，这个估计要怎么给呢？其实是一个很简单的概率问题，假设1代表抛出正面，0代表反面：

img

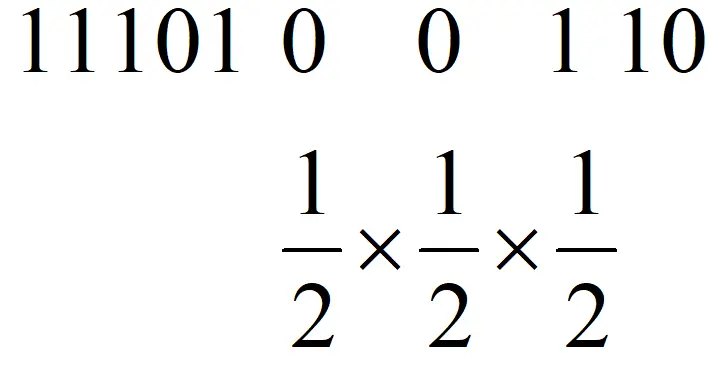
上图中以抛硬币序列”1110100110”为例，其中最长的反面序列是”00”，我们顺手把后面那个1也给带上，也就是”001”，因为它包括了序列中最长的一串0，所以在序列中肯定只出现过一次，而它在任意序列出现出现且仅出现一次的概率显然是上图所示的三个二分之一相乘，也就是八分之一，所以我可以给出一个估计值，你大概总共抛了8次硬币。

很显然，上面这种做法虽然能够估计抛硬币的总数，但是显然误差是比较大的，很容易受到突发事件（比如突然连续抛出好多0）的影响，HyperLogLog算法研究的就是如何减小这个误差。

之前说过，HyperLogLog算法是用来计算基数的，这个抛硬币的序列和基数有什么关系呢？比如在数据库中，我只要在每次插入一条新的记录时，计算这条记录的hash，并且转换成二进制，就可以将其看成一个硬币序列了，如下(0b前缀表示二进制数)：

img

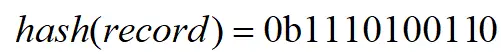
根据上面抛硬币的启发我可以想到如下的估计基数的算法（这里先给出伪代码，后面会有Java实现）：

1
2
3
4
5
6
7
8
9
10
输入：一个集合
输出：集合的基数
算法：
     max = 0
     对于集合中的每个元素：
               hashCode = hash(元素)
               num = hashCode二进制表示中最前面连续的0的数量
               if num > max:
                   max = num
     最后的结果是2的(max + 1)次幂

举个例子，对于集合{ele1, ele2}，先求hash(ele1)=0b00110111，它最前面的连续的0的数量为2（又称为前导0），然后求hash(ele2)=0b10010000111，它的前导0数量为0，我们始终只保存前导零数量的最大值，所以最后max是2，我们估计的基数就是2的(2+1)次幂，即8。

为什么最后的max要加1呢？这是一个数学细节，具体要看论文，简单的理解的话，可以像之前抛硬币的例子那样理解，把最长的一串零的后面的一个1或者前面的一个1”顺手”带上进行概率估计。显然这个算法是非常不准确的，但是这个想法还是很有启发性的，从这个简单的想法跟随下文一步一步优化即可得到最终的比较高精度的HyperLogLog算法。

5.2分桶

最简单的一种优化方法显然就是把数据分成m个均等的部分，分别估计其总数求平均后再乘以m，称之为分桶。对应到前面抛硬币的例子，其实就是把硬币序列分成m个均等的部分，分别用之前提到的那个方法估计总数求平均后再乘以m，这样就能一定程度上避免单一突发事件造成的误差。具体要怎么分桶呢？我们可以将每个元素的hash值的二进制表示的前几位用来指示数据属于哪个桶，然后把剩下的部分再按照之前最简单的想法处理。
还是以刚刚的那个集合{ele1,ele2}为例，假设我要分2个桶，那么我只要去ele1的hash值的第一位来确定其分桶即可，之后用剩下的部分进行前导零的计算，如下图：假设ele1和ele2的hash值二进制表示如下：

1
2
hash(ele1) = 00110111
hash(ele2) = 10010001

img

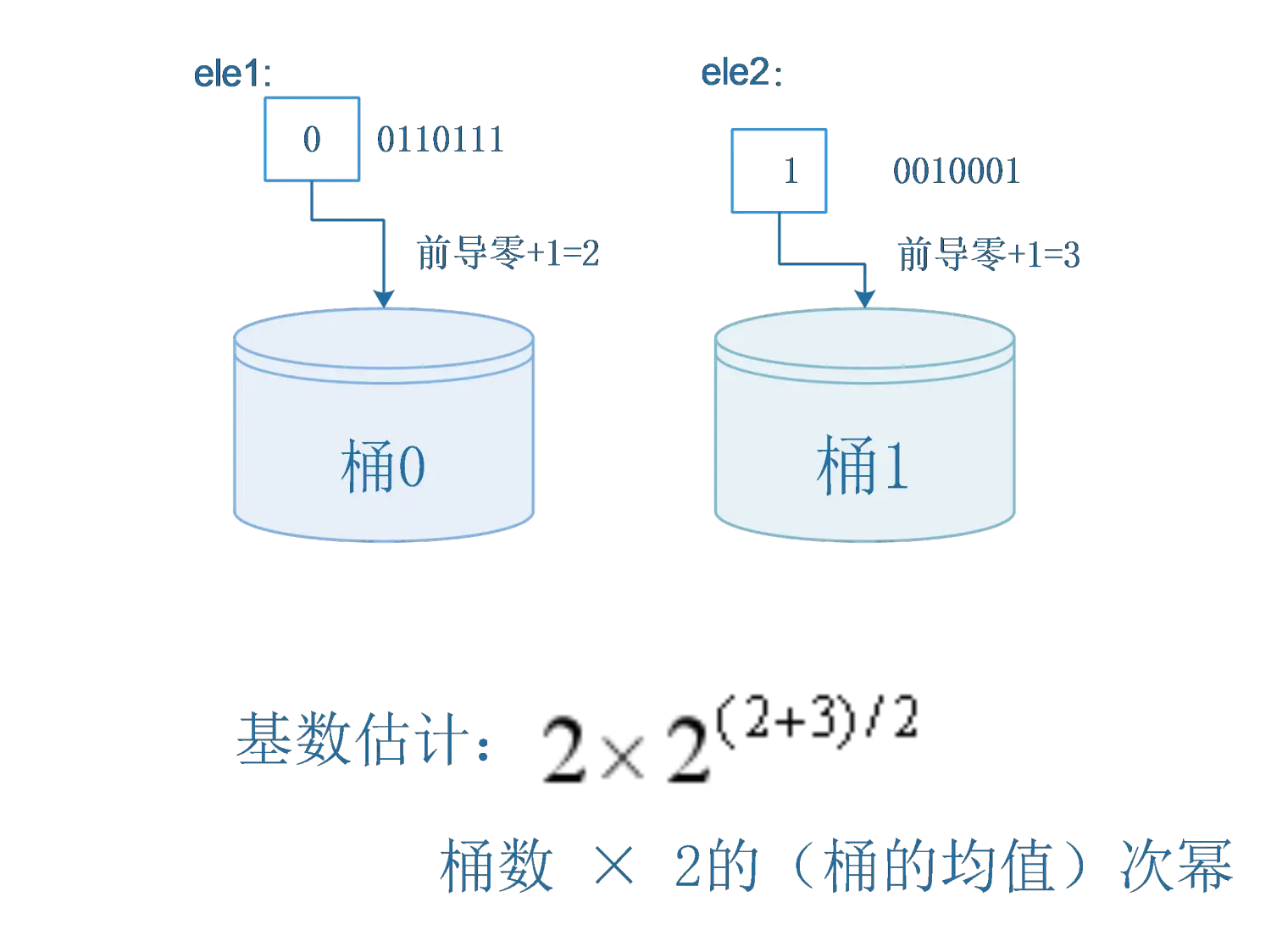
到这里，你大概已经理解了LogLog算法的基本思想，LogLog算法是在HyperLogLog算法之前提出的一个基数估计算法，HyperLogLog算法其实就是LogLog算法的一个改进版。LogLog算法完整的基数计算公式如下：

img

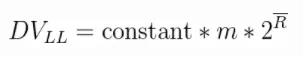
其中m代表分桶数，R头上一道横杠的记号就代表每个桶的结果（其实就是桶中数据的最长前导零+1）的均值，相比我之前举的简单的例子，LogLog算法还乘了一个常数constant进行修正，这个constant具体是多少等我讲到Java实现的时候再说。

5.3调和平均

前面的LogLog算法中我们是使用的是平均数来将每个桶的结果汇总起来，但是平均数有一个广为人知的缺点，就是容易受到大的数值的影响，一个常见的例子是，假如我的工资是1000元一个月，我老板的工资是100000元一个月，那么我和老板的平均工资就是(100000 + 1000)/2，即50500元，显然这离我的工资相差甚远，我肯定不服这个平均工资。用调和平均数就可以解决这一问题，调和平均数的结果会倾向于集合中比较小的数，x1到xn的调和平均数的公式如下：

img

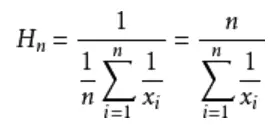
再用这个公式算一下我和老板的平均工资：

img

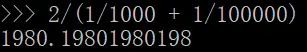
最后的结果是1980元，这和我的工资水平还比较接近，这样的平均工资水平我才比较信服。

再回到前面的LogLog算法，从前面的举的例子可以看出，影响LogLog算法精度的一个重要因素就是，hash值的前导零的数量显然是有很大的偶然性的，经常会出现一两个数据前导零的数目比较多的情况，所以HyperLogLog算法相比LogLog算法一个重要的改进就是使用调和平均数而不是平均数来聚合每个桶中的结果，HyperLogLog算法的公式如下：其中constant常数和m的含义和之前的LogLog算法公式中的含义一致，Rj代表(第j个桶中的数据的最大前导零数目+1)

img

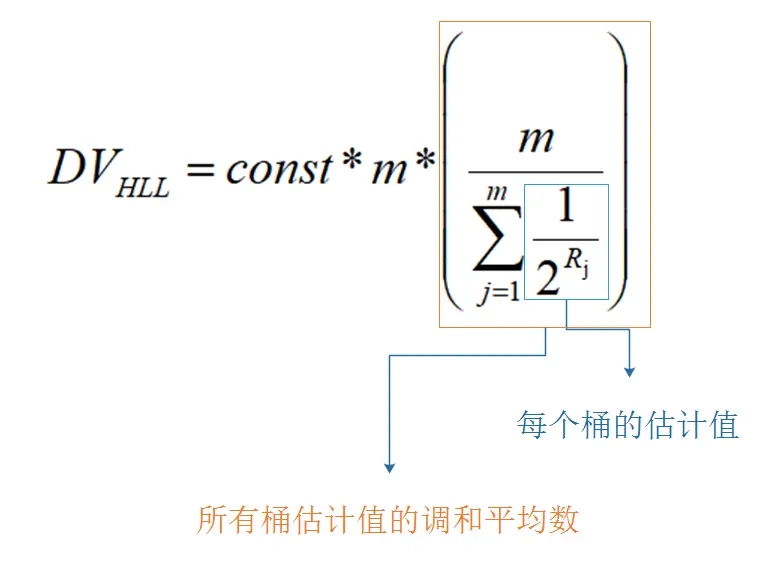
5.4细节微调

关于HyperLogLog算法的大体思想到这里你就已经全部理解了。不过算法中还有一些细微的校正，在数据总量比较小的时候，很容易就预测偏大(大量桶中没有数据，分母整体偏小)，所以我们做如下校正：（DV代表估计的基数值，m代表桶的数量，V代表结果为0的桶的数目，log表示自然对数）

1
2
if DV < (5 / 2) * m:
    DV = m * log(m/V)

我再详细解释一下V的含义，假设我分配了64个桶（即m=64），当数据量很小时（比方说只有两三个），那肯定有大量桶中没有数据，也就说他们的估计值是0，V就代表这样的桶的数目。事实证明，这个校正的效果是非常好，在数据量小的时，估计得非常准确。

5.5constant常数的选择

constant常数的选择与分桶的数目有关，具体的数学证明请看论文，这里就直接给出结论：假设：m为分桶数，p是m的以2为底的对数

img

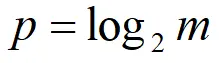
则按如下的规则计算constant

1
2
3
4
5
6
7
8
9
10
switch (p) {
   case 4:
       constant = 0.673 * m * m;
   case 5:
       constant = 0.697 * m * m;
   case 6:
       constant = 0.709 * m * m;
   default:
       constant = (0.7213 / (1 + 1.079 / m)) * m * m;
}

5.6分桶数m的选择

如果理解了之前的分桶算法，那么很显然分桶数只能是2的整数次幂。如果分桶越多，那么估计的精度就会越高，统计学上用来衡量估计精度的一个指标是“相对标准误差”(relative standard deviation，简称RSD)，RSD的计算公式这里就不给出了，百科上一搜就可以知道，从直观上理解，RSD的值其实就是（(每次估计的值）在（估计均值）上下的波动）占（估计均值）的比例（这句话加那么多括号是为了方便大家断句）。RSD的值与分桶数m存在如下的计算关系：

img

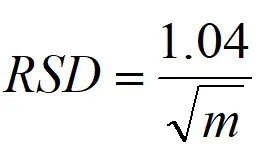
有了这个公式，你可以先确定你想要达到的RSD的值，然后再推出分桶的数目m。

5.7合并

假设有两个数据流，分别构建了两个HyperLogLog结构，称为a和b，他们的桶数是一样的，为n，现在要计算两个数据流总体的基数。

1
2
3
数据流a："a" "b" "c" "d"  基数：4
数据流b："b" "c" "d" "e"  基数：4
两个数据流的总体基数：5

从前文我们可以知道，HyperLogLog算法在内存中的结构其实就是一个桶数组，需要先用下面的算法从a和b的桶数组中构建出新的桶数组c，其实就是从a,b的对应位置取最大的：

1
2
3
4
5
6
7
8
输入：桶数组a，b。它们的长度都是n
输出：新的桶数组c
算法：
     c = c[n];
     for (i = 0; i < n; i++){
         c[i] = max(a[i], b[i]);
     }
     return c;

之后用桶数组c代入前面的算法即可得到合并的总体基数。

5.8Redis中的实现

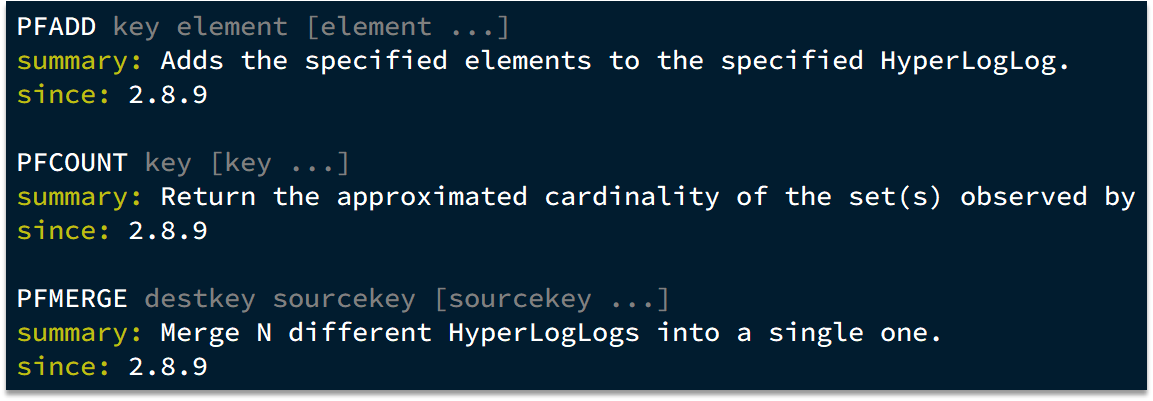
Redis中和HyperLogLog相关的命令有三个：

  • PFADD hll ele

    ：将ele添加进hll的基数计算中。流程：

    • 先对ele求hash（使用的是一种叫做MurMurHash的算法）
    • 将hash的低14位(因为总共有2的14次方个桶)作为桶的编号，选桶，记桶中当前的值为count
    • 从的hash的第15位开始数0，假设从第15位开始有n个连续的0（即前导零）
    • 如果n大于count，则把选中的桶的值置为n，否则不变

  • PFCOUNT hll：计算hll的基数。就是使用上面给出的DV公式根据桶中的数值，计算基数

  • PFMERGE hll3 hll1 hll2：将hll1和hll2合并成hll3。用的就是上面说的合并算法

Redis的所有HyperLogLog结构都是固定的16384个桶（2的14次方），并且有两种存储格式：

  • 稀疏格式：HyperLogLog算法在刚开始的时候，大多数桶其实都是0，稀疏格式通过存储连续的0的数目，而不是每个0存一遍，大大减小了HyperLogLog刚开始时需要占用的内存
  • 紧凑格式：用6个bit表示一个桶，需要占用12KB内存